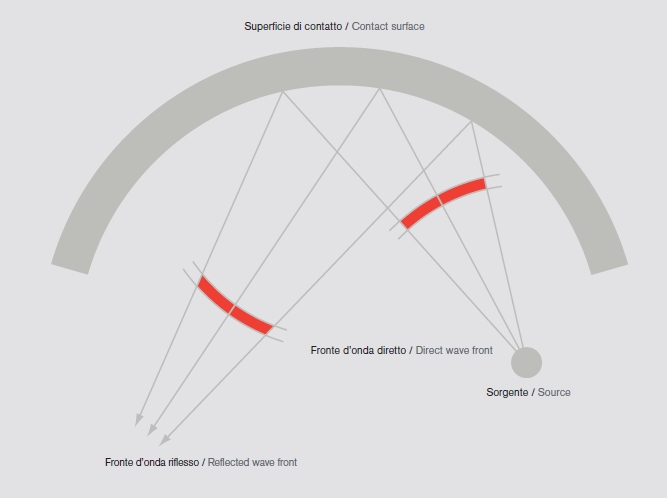
Riverberazione: è il perdurare di un suono all’interno di uno spazio confinato successivo al completo esaurimento della sorgente che lo ha generato ed è causato dalle riflessioni multiple sulle superfici che delimitano l’ambiente stesso.
“… quando incontrano qualche ostacolo, le prime onde, refluendo all’indietro, intersecano le seguenti e ne turbano i contorni.
In modo analogo, anche i suoni si propagano tutto all’intorno circolarmente; ma mentre nell’acqua le onde si muovono soltanto allargandosi sul piano della superficie dello specchio acqueo, i suoni non solo si diffondono orizzontalmente, ma salgono gradatamente anche in altezza”.
Vitruvio Pollio “De Architectura”, Libro V, tratto dagli scritti di Aristosseno (ca. 350 a.C.)
La geometria del suono
L’evoluzione e lo sviluppo della vita degli esseri umani sono associati a fenomeni di natura sensoriale e questi eventi si manifestano attraverso il dono meraviglioso della percezione dei cinque sensi principali caratterizzando il modo di vivere di ogni individuo, dal momento della sua nascita per tutto il ciclo vitale.
L’apparato uditivo è considerato uno degli organi più complessi e sofisticati del corpo umano. Al suo interno sono racchiusi dei meccanismi meravigliosamente affascinanti, dove l’energia potenziale che si sviluppa nell’ambiente circostante attraverso la voce, i suoni, i rumori e qualsiasi altra agitazione dell’aria, viene trasformata in segnale acustico.
D’altronde, il suono e il rumore sono perturbazioni e spostamenti, più o meno grandi, di particelle che si propagano agevolmente se veicolate da mezzi elastici gassosi, liquidi o solidi che siano.
In assenza di questi, cioè nel vuoto, il suono non ha possibilità di diffondersi, mentre trova la sua genesi naturale nell’aria, nell’acqua, nel cemento o nell’acciaio e in generale in presenza di mezzi di propagazione.
L’espansione del suono avviene dunque in mezzi molto diversi tra loro per aspetto, stato di aggregazione e conformazione fisica.
L’onda sonora generata dalle perturbazioni è in sostanza un movimento meccanico, un’energia a tutti gli effetti, chiamata tecnicamente pressione sonora.
Questa energia sposta materialmente la membrana timpanica (incudine, martello e staffa), attraversa la coclea, che contiene i liquidi dove sono presenti le cellule ciliari (neuromediatori), viene trasformata in segnale e trasmessa al cervello attraverso l’VIII nervo cranico che è il nervo acustico.
È evidente che il corpo umano e i meccanismi che lo compongono e lo animano ci appaiono inevitabilmente come un qualcosa di straordinaria bellezza per la loro semplicità, funzionalità e purezza. Di fronte a simili fattezze, come esperti in acustica architettonica, dobbiamo sentire l’obbligo morale e professionale di preservare l’apparato uditivo dai pericoli ai quali, suo malgrado, esso andrà incontro e di applicarci nella ricerca per poter conferire a tutte le tipologie di ambienti, da quelli più semplici domestici a quelli più complessi e di utilizzo di massa, degli elevati standard qualitativi di comfort acustico. Questo perché le suggestioni uditive non derivano soltanto dalle voci o dai suoni musicali ma anche semplicemente da rumori meccanici, e i rischi ai quali è sottoposto l’udito possono derivare sia da situazioni di rumori particolarmente intensi, sia da specifiche condizioni d’ascolto sfavorevoli e protratte nel tempo.
I danni uditivi sono di diversa natura e quelli più gravi e purtroppo irreversibili interessano i delicatissimi meccanismi (come le cellule ciliate contenute nella coclea) di natura neuronica che una volta danneggiati, non si riproducono mai più.
Ed è proprio per questo che una delle aree di applicazione degli studi del Centro Ricerche Fantoni è tesa specificatamente all’individuazione e soluzione dei problemi che si manifestano negli ambienti riverberanti – ambienti chiusi – che si differenziano principalmente dalle situazioni all’aperto, per il fatto che in tutti gli spazi confinati vi è la presenza, oltre che del suono diretto, proveniente da una o più sorgenti, anche di tutte quelle riflessioni che si generano in funzione della geometria architettonica degli ambienti e dei materiali di cui sono composti.
Nel restituire alle persone ambienti dalle elevate risposte al segnale acustico, più che esprimerci nel nostro ambito solo in termini di decibel (che non è l’unità di misura del suono, bensì una sua scala di lettura), bisogna concentrare l’attenzione anche su cosa succede all’interno di un ambiente. Qui, infatti, le perturbazioni di pressione sonora si diffondono dalle pareti, dal soffitto, dal pavimento e da qualsiasi altro elemento presente in una sala, interessando da vicino tutte le frequenze possibili e dando così origine ad una serie di riflessioni, non sempre facilmente controllabili, e ad altri fenomeni acustici di disturbo.
I riferimenti storici principali sono gli ambienti denominati “sabiniani”, in omaggio a Wallace Clement Sabine (1868-1919), fisico statunitense, pioniere dell’acustica architettonica e studioso delle prime relazioni analitiche riguardanti il tempo di riverberazione (RT60), considerato – insieme ad altri indicatori da non trascurare – uno degli elementi di studio fondamentali ed essenziali per l’equilibrio acustico complessivo di tutti gli ambienti, da tenere quindi opportunamente sotto controllo.
Per dare un’idea su che cos’è il tempo di riverberazione – non tanto da un punto di vista tecnico ma di pura percezione – si provi a pensare alla sensazione acustica che si può sperimentare quando ci si trova all’interno di una chiesa o di una palestra e si cerca di parlare. Non sarà di certo la stessa impressione che potremo avere in una sala cinematografica o in uno studio di registrazione. Pensiamo, inoltre, al fastidioso “rimbombo” all’interno di un capannone industriale, che non ci consente di sentire bene e neanche di comunicare correttamente. Tutto ciò non può essere assolutamente paragonato alla precisione di ascolto all’interno di un teatro, di una sala conferenze o comunque in ambienti con caratteristiche di progettazione acustica corretta.
Diverse sono poi le esigenze di ascolto: se dobbiamo ascoltare un concerto di canti gregoriani avremo bisogno, ad esempio, di un ambiente con riverberazione particolarmente lunga (caratteristica tramandata nei secoli dagli ordini religiosi) con tempi di quattro, cinque secondi ed oltre perché questo tipo di canto, per essere apprezzato non può avere tempi inferiori in quanto perderebbe la propria particolarità.
Al contrario, in uno studio televisivo o in una sala cinematografica, c’è la necessità di avere ambienti particolarmente “secchi” con tempi di riverberazione ridotti addirittura a mezzo secondo.
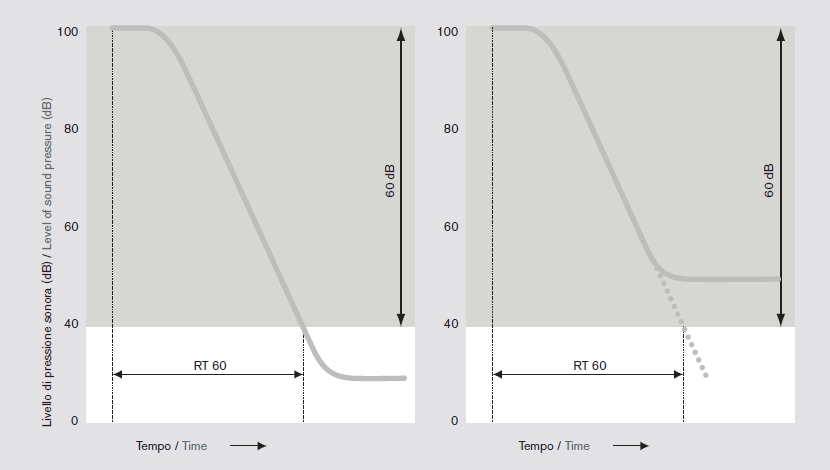
Il tempo di riverberazione si definisce tecnicamente come “il tempo necessario affinché un suono presente all’interno di uno spazio confinato diminuisca di 60 dB”, e in termini più semplici, lo si può indicare come “il tempo necessario affinché un’emissione sonora particolarmente elevata (sempre in ambiente chiuso) vada a diminuire la propria intensità fino a diventare praticamente impercettibile”.
L’equazione matematica che Sabine scrisse sul tempo di riverberazione verso la fine dell’Ottocento, fu ricavata in maniera assolutamente sperimentale: egli confermò le proprie intuizioni lavorando all’interno di una stanza – che possiamo pensare come l’antenata della camera riverberante – utilizzando quale sorgente un organetto a manovella invece di una sorgente omnidirezionale o dodecaedrica dei giorni nostri, un cronometro al posto di sistemi digitalizzati ed un buon orecchio invece di evoluti microfoni.
Le operazioni principali che si svolgevano nella pseudo camera riverberante consistevano nel posizionare e rimuovere dei cuscini imbottiti e nel misurare il tempo che intercorreva tra l’interruzione della sorgente e il completo dissolvimento del segnale acustico.
Tutto questo portò Sabine a fissare matematicamente uno dei concetti fondamentali dell’acustica architettonica, attraverso la seguente relazione ancor oggi valida:
fig. 1 RT60 = 0,161 V/S. a
Dove con “RT60” si indica il tempo di riverberazione misurato in secondi, con “V” il volume della stanza in metri cubi, con “S” la superficie della stanza in metri quadrati e con “a” il coefficiente di assorbimento medio delle superfici che compongono la stanza (fig. 1).
Si può intuire come il perdurare di una coda sonora all’interno di spazi chiusi generi difficoltà nell’ascolto, non solo della musica (composta da suoni molto variabili nella loro complessità), ma anche del parlato.
Ed è per questo che si può affermare che non esiste in realtà un tempo di riverberazione ottimale di riferimento, ma lo si dovrà ricercare sicuramente in un intervallo più ampio di tempi compresi fra una condizione particolarmente secca, presente all’aperto (campo acustico libero) o nelle stanze anecoiche (senza riverberazione), ed una con esagerata riverberazione prodotta dai grandi volumi architettonici.
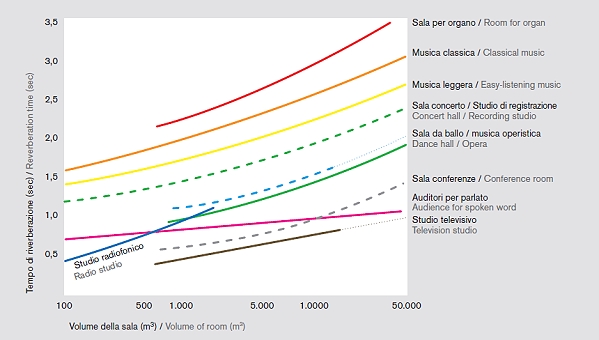
Studi recenti integrano la valutazione del tempo di riverberazione con una serie di analisi sull’ascolto e sul giudizio personale dei singoli spettatori. Il diagramma di seguito inserito rappresenta schematicamente la determinazione del tempo di riverberazione indicativo, in base alla funzione e al volume complessivo di un ambiente (fig. 2).
fig. 2 Determinazione grafica del tempo di riverberazione in funzione del volume complessivo degli
ambienti e della loro diversa destinazione d’uso.
Affinché un ambiente sia dotato di una buona acustica e di un tempo di riverberazione caratterizzante, è necessario che le riflessioni sonore siano ripartite in modo omogeneo in tutto il volume architettonico. Di conseguenza la geometria di una sala assume un ruolo importante perché è proprio dalla forma strutturale, dai materiali d’impiego, dalle opportune inclinazioni della sala stessa e dai pannelli di spinta del suono che si riescono ad ottenere situazioni di ascolto significative, cercando di evitare in ogni modo le aree di eco e di silenzio dovute ad ombre sonore.
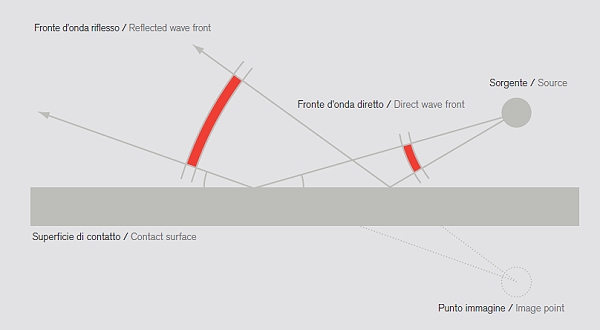
Le riflessioni generate dalle onde sonore seguono gli stessi principi geometrici di quelle originate dai raggi di luce che colpiscono uno specchio, dove l’angolo di incidenza del fronte d’onda diretto è uguale all’angolo di riflessione. Di conseguenza la geometria piana ci offrirà una sorgente, un punto immagine, e un angolo di “rimbalzo” dell’onda, determinato dalla forma della superficie di impatto (fig. 3).
fig. 3 Rappresentazione grafica della riflessione geometrica del suono su superficie piana.
Le superfici delle sale vengono investite senza distinzione da fronti d’onda sferici – non come si pensa, per semplicità, da raggi lineari – e questi fronti subiscono nel loro percorso molte riflessioni dato che si diffondono di continuo su tutte le pareti.
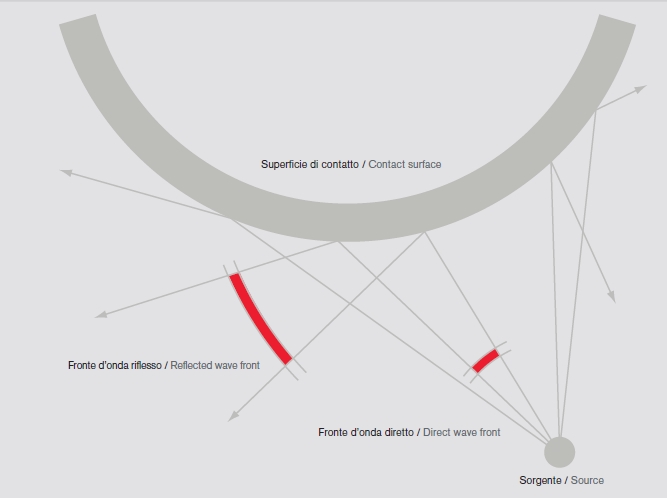
Se un’onda sonora, viceversa, colpisce una superficie non piana, ma concava o convessa, le riflessioni tenderanno a fenomeni di concentrazione o diffusione (fig. 4-5).
fig. 4 Rappresentazione grafica della riflessione geometrica del suono su una superficie convessa. Superficie convessa = Diffusione del suono.
fig. 5 Rappresentazione grafica della riflessione del suono su una superficie concava.
Superficie concava = Concentrazione del suono.
L’effetto prodotto da questa progressione delle onde sonore comporta la perdita di energia da parte di ogni singola riflessione fino alla sua completa dissipazione in calore. Le riflessioni che seguono questo tipo di andamento interessano le frequenze percettibili medio-alte e sono chiamate frequenze speculari.
Di conseguenza bisognerà, in fase di progettazione acustica, controllare la direzione ed il comportamento del suono seguendo le regole basilari della riflessione geometrica per non compromettere la buona riuscita degli ambienti.
Cercando poi di guardare più da vicino il comportamento delle frequenze e le condizioni di operatività che dobbiamo riservare all’acustica architettonica e per meglio conoscere la composizione dei nostri antagonisti principali, cioè suoni e rumori, dobbiamo innanzitutto sapere che cos’è una frequenza, qual è il suo campo d’azione e la sua morfologia.
Bassa Frequenza
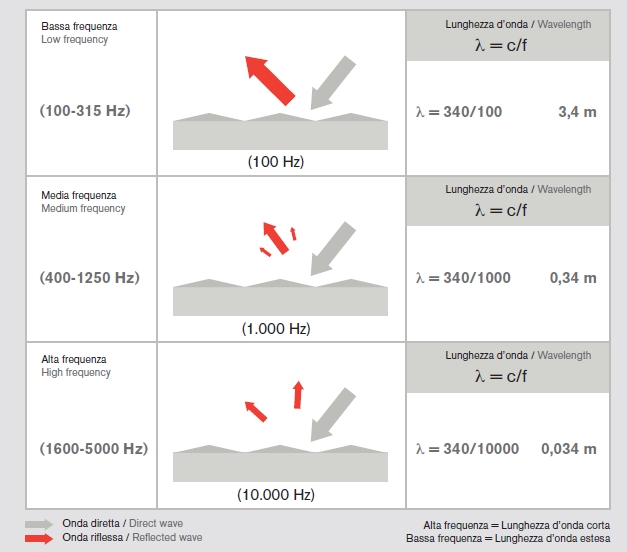
La bassa frequenza è una frequenza di natura impattiva e non è in grado di sentire le asperità della parete; tutto quello che trova nel suo cammino viene colpito con la stessa potenza.
Tanta energia colpisce la parete ed altrettanta energia rimbalza (in acustica “riflette”) seguendo una direzione di riflessione con un angolo uguale a quello di impatto.
Per chiarire il concetto, si può associare l’onda sonora ad una certa quantità d’acqua. Se, infatti, lanciamo con forza un secchio pieno d’acqua, quindi una certa massa, su di una parete, osserveremo che gran parte dell’acqua che colpisce il muro avrà la forza necessaria per riflettersi in altre direzioni perdendo poca dell’intensità d’impatto data la sua forza iniziale. Ora, è importante sapere come si sviluppa la lunghezza d’onda della bassa frequenza. Sappiamo che la lunghezza d’onda di una frequenza è data in generale dalla seguente relazione analitica:
λ = c/f
Dove con “c” indichiamo la velocità del suono nell’aria (340, 341, 342 m/sec …), e con “f” la frequenza di riferimento. Ricordandoci che il range di valori percepibili dall’apparato uditivo degli esseri umani varia tra i 16 e 16.000 Hz, ed ipotizzando di prendere in considerazione una bassa frequenza di 100 Hz (equivalenti all’oscillazione di una particella per 100 volte nell’unità di tempo, ossia il secondo [sec.]) avremo:
λ = 340/100 = 3,4 m
Come potete osservare, la bassa frequenza è dotata di una estesa lunghezza dell’onda, (perché in acustica 3,4 m sono una lunghezza non indifferente) e questa è la sua caratteristica principale capace di mandare in vibrazione intere pareti.
Se prendiamo in considerazione i moti rotazionali (come per esempio quelli di un motore) con frequenza di 34 Hz, la lunghezza d’onda sarà addirittura:
λ = 340/34 = 10 m
Media frequenza
Se ora lanciamo sulla parete lo stesso quantitativo d’acqua ma questa volta con una bottiglia, avremo un urto del tutto inferiore a quello precedente ed è intuitivamente chiaro che l’impatto delle medie frequenze su qualsiasi superficie sarà più attenuata della bassa frequenza e la direzione delle onde riflesse seguirà una direzione del tutto diversa dalle precedenti, assumendo un andamento di tipo composto (come rappresentato nello schema funzionale).
E la lunghezza d’onda, supponendo una media frequenza pari a 1.000 Hz, sarà:
λ = 340/1.000 = 0,34 m = 34 cm
Si può notare come la lunghezza d’onda a media frequenza sia sensibilmente diminuita rispetto a quella della bassa frequenza.
Alta frequenza
Proseguendo con le esemplificazioni, dopo l’acqua lanciata con il secchio e con la bottiglia vogliamo ulteriormente esagerare cercando in qualche maniera di proiettare ancora la stessa quantità d’acqua con una siringa.
La parete, ovviamente, non avrà nessun tipo di deformazione ma noteremo che le gocce d’acqua più o meno lentamente seguiranno l’andamento delle asperità presenti sulla sua superficie, riflettendosi in direzioni del tutto diverse l’una dall’altra.
L’alta frequenza ha quindi un tipo di comportamento per cui si può considerare come un’onda “intelligente”, nel senso che “sente” tutte le scabrosità di una parete, e non solo, seguendo anche gli andamenti determinati dai materiali e dalla morfologia strutturale e spaziale delle superfici.
Supponendo un’alta frequenza pari a 10.000 Hz avremo:
λ = 340/10.000 = 0,034 m = 3,4 cm
Si è osservato dunque l’importanza di una serie di aspetti che necessariamente siamo tenuti a prendere in considerazione quando parliamo di ambienti chiusi e di campo riverberante in generale.
Approfondendo poi gli aspetti geometrici e i principi che regolano la propagazione delle onde sonore, credo si sia acquisita una certa “dimestichezza” anche con le frequenze.
Le argomentazioni trattate vogliono essere uno strumento conoscitivo iniziale per chi si avvicina per la prima volta al tema sempre più sentito del corretto funzionamento acustico degli ambienti, nel contesto di un’argomentazione comunque vastissima.
Controllare tutti questi interessanti elementi e “normalizzare” il tempo di riverberazione, significa lavorare a stretto contatto con una serie di parametri acustici che sono decisivi per “l’accordatura” finale delle sale. Vuol dire confrontarsi, inoltre, con le frequenze e con i coefficienti di assorbimento dei materiali, siano essi di uso comune o tecnologicamente avanzati, significa modellare geometricamente lo spazio architettonico, le sue regole di partizione e decidere quali saranno i tempi (RT60) che più si adatteranno alle diverse tipologie che gli ambienti dovranno assumere, asservendoli alle esigenze funzionali più differenti.
Sarà altrettanto importante riflettere sulle ricerche condotte nei tempi passati da coloro che, avuti i nostri stessi problemi, hanno cercato di risolverli senza avere a disposizione gli strumenti altamente sofisticati dei giorni nostri e di conseguenza mettere in atto una ricognizione temporale alla ricerca degli ambienti più significativi presenti nella letteratura acustica, dai quali trarre, oggi, riferimento e opportunità per sviluppi di successo.